Starting in March 2020, I began a large stream project to model a comprehensive, highly-detailed Caterpillar 434E backhoe. Please watch the first stream (first 3 minutes of abridged version at least) for an overview.
It's a straight-forward project of building a complex model over an extended period of time. The spin on the project is that I want your help to accomplish it! If I build some parts and you build some parts, we will finish this thing much quicker. Plus the contribution format will include reviews, the potential of having your piece(s) assimilated into the final model. Not to mention large quantities of XP are at stake 🤑
NOTE: This is an involved project reserved for Citizen members.
The general idea is that I kickoff stages of the project via live stream, which is typically once per month. For the time in between streams, you choose a piece of the backhoe and apply what you learned from the stream to that piece. For example, the first stream covered initial block out. So between stream 1 and stream 2, your job is to pick a piece and block it out.
This is the repeating protocol for each Assignment Period (between-streams):
I will reply to this thread after each stream with a [big] assignment post denoted by a 📣 emoji in the title. There I will clarify instructions about each Assignment Period.
We will centralize our collaborative communication between the streams and this thread. Ask any and all questions pertaining to the Backhoe project here.
Iv'e added my links to the sheet, because I think @theluthier will probably use it for XP purposes.
duerer about those two videos on your to-watch list: the first one (Numberphile) is great, but I'd avoid the second one if I were you (haven't seen that one, so...); that's a 4d hypersphere one that will probably just confuse you and saying in the title that a quaternion is a 4d number is complete and utter nonsense: there are no 4d numbers. Numbers have dimension 0 when they have a dimension at all. Like a point in 3D space; the point is not a 3 dimensional point! It is a point in 3D space!
Yes he still wants is to submit based on his last official forum posting.
plus I think it is a good way to judge who is still capable of working on this project.
It will help us masters of looses ends figure out what needs to be done too!
ok question do we upload as linked or just normal? lol I got confused on that issue.
I think we just have to comment on the sheet that you finished your part, your file is already uploaded in Google Drive anyways.
Thank you, spikeyxxx, for the watch recommendation. The second one looks indeed already complicated in the preview image although I like it from an aesthetic point of view 😉.
PS: spikeyxxx Could I say that a complex number can be visualized as a point in 2-D space with one coordinate beeing the real part and the other the imaginery part? And the quaternion would then be "visualized" 😉 as a point in 4D-space on a 4D-hypersphere?
Could I say that a complex number can be visualized as a point in 2-D space with one coordinate beeing the real part and the other the imaginery part?
Absolutely! But remember that this 2D space is not a subspace of our known 3D space; it takes 1 dimension from our 3D space (the real part) and one from another, imaginary space.
And the quaternion would then be "visualized" 😉 as a point in 4D-space on a 4D-hypersphere?
NO! (Technically: I could say that, but I wouldn't(, because it is very likely to be misunderstood and nobody knows what a 4D hypersphere looks like anyway) and you can't say that...)
It can be seen as a point in a 4 dimensional space, but that is not our 3D plus one more dimension (something like spacetime is our 3D world plus one...)!
It is an imaginary 3D space plus one real dimension!
To say something like: "A complex number is a 2D number" (and I know I've said that myself...)is actually short for something like: "A complex number is an element of C (the collection of complex numbers) and C is homeomorph to R (the collection of real numbers) * R = R² and can therefor be represented as a 2 dimensional vector."
Homeomorph here means that there exists a one-to-one mapping between the two.
In (mathematical) topology we say that for instance a donut is homeomorph to a coffeecup (you can think of topology as 'geometry without a distance'. If two points are 'connected' in one, then they are 'connected' in the other), although they are obviously not the same (try pouring coffee in a donut...).
My advice: Do not try to visualize a quaternion and save yourself a truckload of problems!
@theluthier The MASTER_dog-434e_model-assembly doesn't have a collection for my ARTIFACT_dog-434e_engine-enclosure_MASTER part so I couldn't really see how my enclosure fits in with the rest of the Dog. Nonetheless I don't expect any collision with blanchsb digger arms or the chassis from @adrian2301 as I referenced both. Fingers crossed.
Good question @adrian2301. I appreciate the continued comment approach because it represents an "official" submission where the submitter and I are on the same page. Though I don't need a URL anymore since we're all syncing. Like dostovel said, a simple "I'm done with my part" or "submission is ready" or "the eagle has landed" will suffice!
Sorry I know it's a bit redundant for submitters 😕
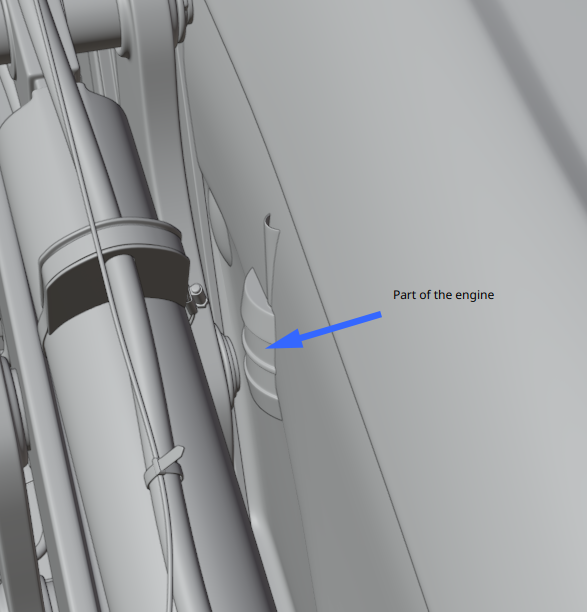
aartifact I've just saved a new version of the master assembly file with your engine enclosure collection linked. It's looking really nice! Contours are crisp and seem quite accurate to the real thing.
I only spotted one intersection with @adrian2301's engine on the starboard side:
Thank you, spikeyxxx, for these precise explanations. Although it's certainly no easy subject, it's makes me curious and I wish to know more about it because I don't only want to push buttons but understand what I'm doing there. Quaternions are certainly worth to be treated in their own thread.
I'm glad Kent made the Google Drive folder for the files, if it had been up to me I'd probably make 4 different folders for the files to live in and name them after the Hogwarts houses. And then Kent in the livestream would be like, Adrian Engine will be in...... Griffindoroooorf!
To be clear: you normally would never try to visualize a number (if you feel the urge to do that, then that is probably a left-over urge from when you first learned about numbers by counting buttons or apples or cakes or sheep...which results in a really clumsy way of adding two integers (counting five apples, counting three apples, putting them together on one heap and counting them again) and getting ridiculous as soon as you get negative numbers...or fractions: divide one cake by four people, WTF! Then how do I divide two bananas by three carrots or one apple by seven sins? No wonder children have problems with learning to calculate...), say you have to calculate 5 * 3, you don't imagine two points on a line, representing 3 and 5 respectively, now do you? And how would you visualize the multiplication?
The only reason we do that (visualizing numbers) with the complex numbers is to show that a multiplication in C describes a rotation and therefore a 2D rotation can be described as a multiplication of complex numbers. Once you understand that, it is a 'small' step to understand that a 3D rotation can be described by the multiplication of quaternions (again: quaternions are numbers!).
I will have a look and see what can be done. Won't be today but consider it taken care off.
I have made some progress with the hydraulics around the swing frame today, 
jakeblended achieved a good stage, only maybe some tweaks here and there, and finish the hydraulics.
