Get it? Math Lab.... sounds like Me.... Lab?.... No? ok
So 
spikeyxxx you're like a super mathematician, I'm doing the Blender Cloud Procedural Shading course and it is super heavy dense in tough, difficult and impossible things and worst of all there's like a lot of math involved. I wanted to use this to bother you a lot and ask you math questions when it comes to procedural shading.
The course is good but Simon goes way too fast and doesn't get into the really basics and assumes you know what happens mathematically under the hood.
*WARNING, HERE BE MATH*
I'm trying to understand the pattern duplication:
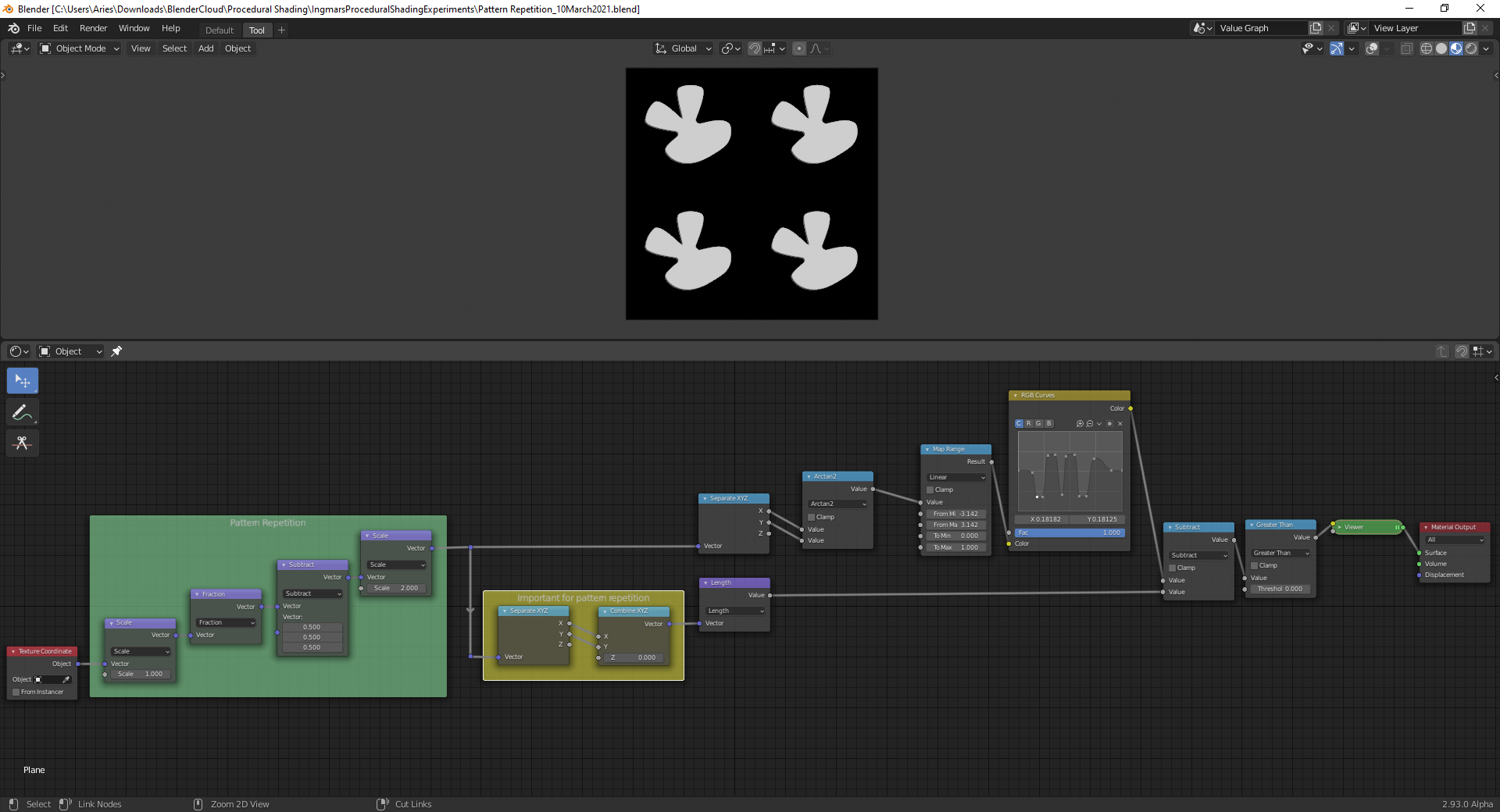
What are the green and yellow frames doing exactly and why do I need the yellow frame for making the green frame work? File is here.
Okay, with the "Viewer Node", I can visualize the field separation (here into 4 fields):
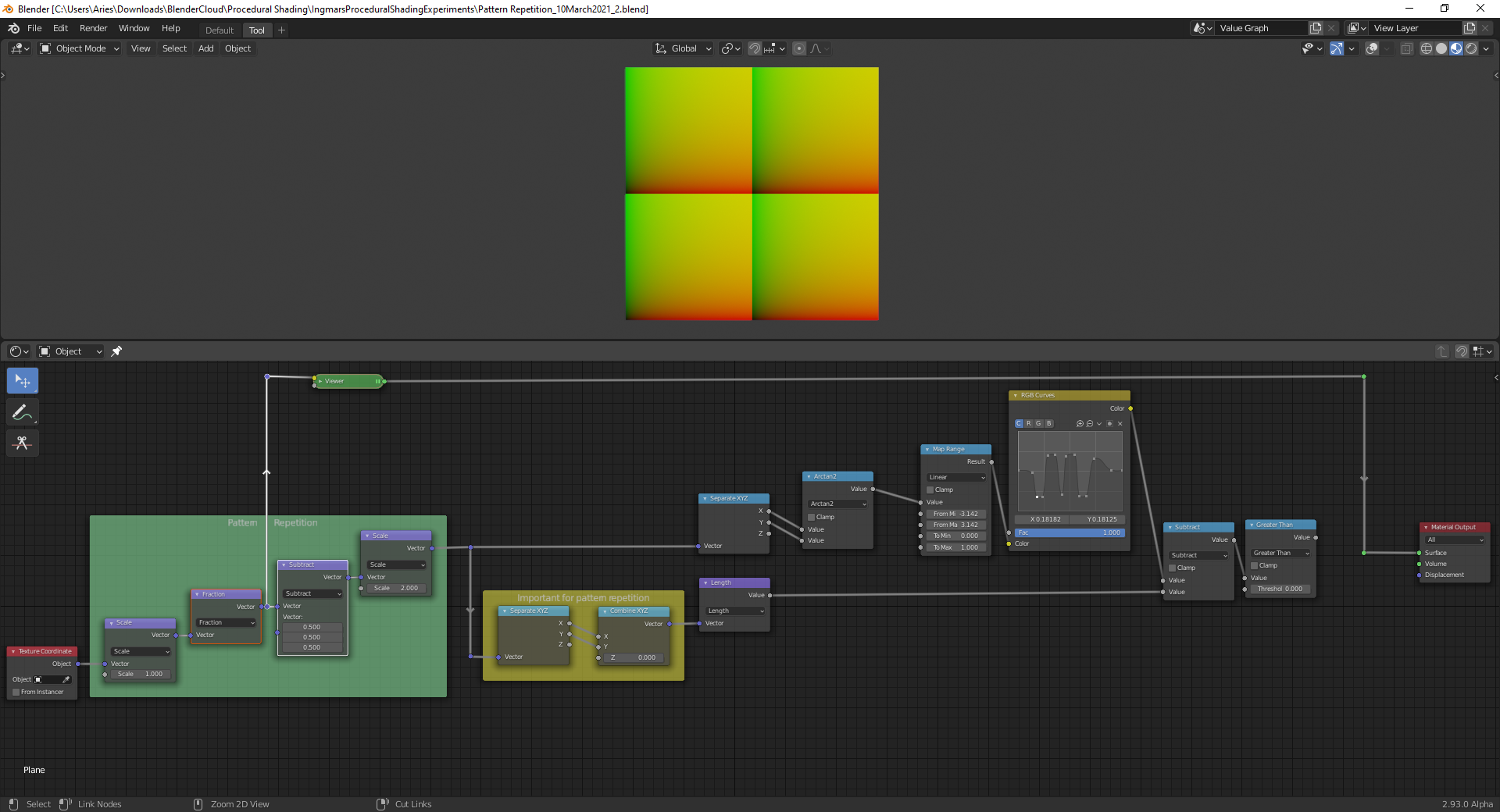
But why does it work like this?
I don't know dude, I'm not that far in. I watched a lot of chapters before I decided that I needed to step back and understand it to the core before continuing. I'll get to where you are eventually.
Okay, look at the green frame first. from left to right: the first node does nothing when set to 1 (it multiplies all values by 1), so after that we still have the normal Object coordinates (I only write some of the X- values so it doesn't get too cluttered):
Then we get the Fraction Node, that does this:
Watch the unexpected way it takes the fraction of negative numbers, but this is advantageous for us.
Then we subtract 0.5 from all values:
And finally multiply by 2 to get:
This way we now have 4 fields with the original Object Coordinates.
If we increase the value in the first Scale Node, we create more, smaller fields like that.
The yellow frame is just to get rid of the Z-values.
Here is an alternative (and 'cheaper', more intelligent) way to get rid of the Z problem:
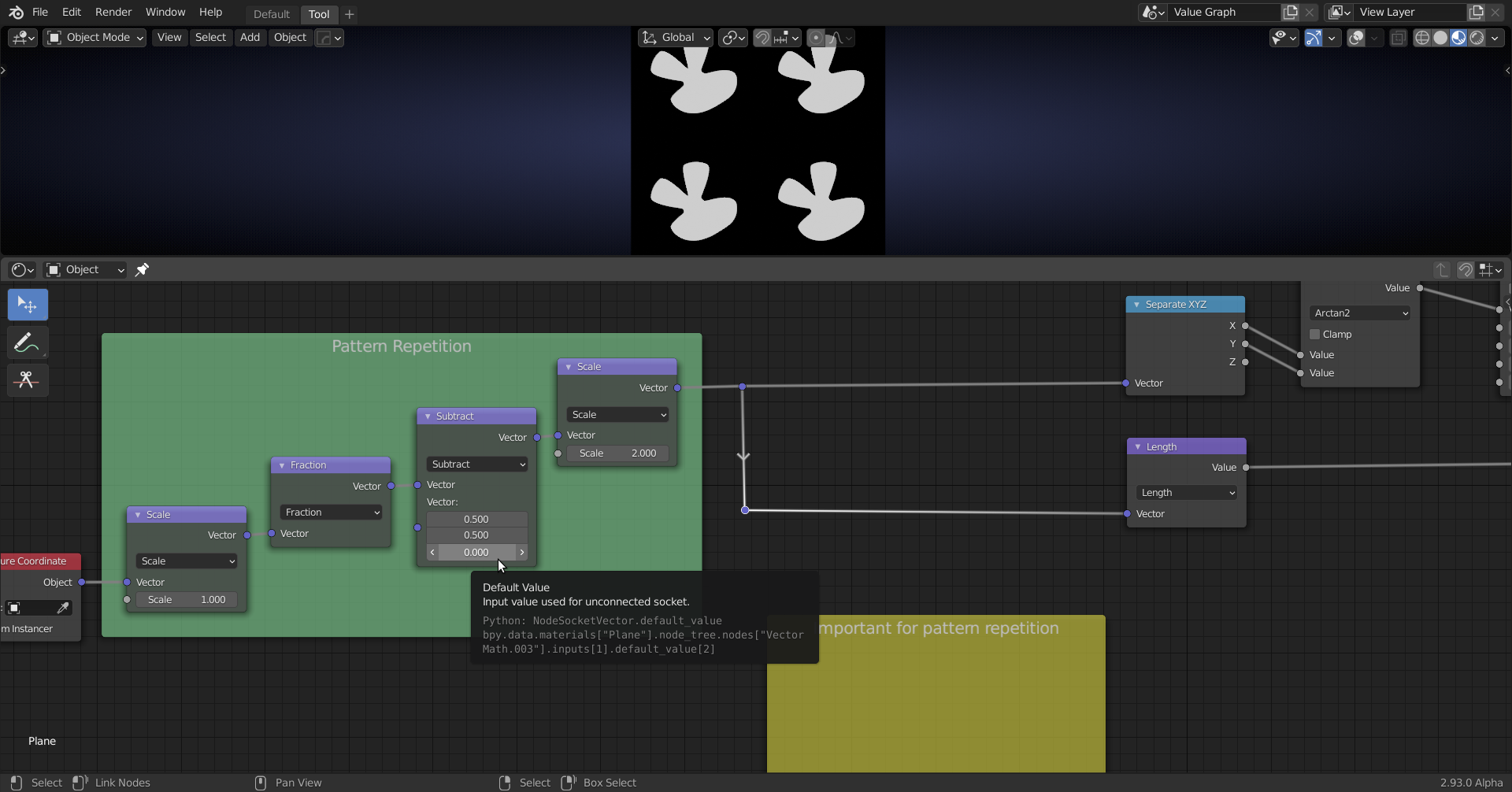
Because on a Plane the Object's Z is always 0, but we subtracted 0.5 and then multiplied by 2, making the Z always -1.
When you then calculate the length, you get the square root of (x²+y²+z²),which is the square root of (x²+y²+1) and we want the square root of (x²+y²+0).
Man I'm looking forward to the day I'm like, no Spikey, it's actually (x-y*z) and you're like, oh dude yeah, you're right, thanks.
Thanks, spikeyxxx, for the explanations 😀! Now, it's clear 👍! I didn't expect that "Fraction" works for negative numbers as you described it. Is there a mathematical explanation or is it "just" defined like this in order to continue the pattern from the positive numbers with the negative numbers?
spikeyxxx, your method for setting the vector's z-coordinate to zero is obviously smarter since it saves two nodes. Simon Thommes introduces this "zeroing" first (when it has not effect) and then demonstrates how to create a repetitive pattern so that he effectively does the second step before the first one which I find confusing. Thank you again for the clarifications 👍!
spikeyxxx For calculating a random value for each tile of the pattern repetition, Simon Thommes makes use of the "Snap Operator" of the "Vector Math Node". The "Blender 2.92 Manual" here describes it like this:
Snap
The result of rounding A to the largest integer multiple of B less than or equal A.
I understand it like this:
If we have for example a vector A = (4.73, 3,51, 9.48) and vector B = (1, 7, 3), then the result As (="A snapped") should be:
As = (4, 0, 9)
Did I understand it correctly?
And what if vector B also has decimal fractions? Does "largest integer multiple of B" mean rounding the entries of B before the multiplication or are the decimals in the coordinates of B simply cut off?
Ok Spikey, I learned my lesson and made a graph for multiplication with less squares and made all the calculations. It's incredible, I can clearly see now why multiplication would be use when you want to repeat a pattern, the values mirror each other. This is awesome.
Great questions like always duerer
Fraction seems to do the following: the Fraction of a number a is: a minus the Floor of a. (the Floor always rounds down to the nearest integer, so the Floor of -0.5 is -1.
I do not know the mathematical definition, but I'm sure it's not used like this in math.
Modulo is one that I don't know what it does exactly; it has nothing (or very little) to do with the mathematical modulo.
Snap??? I've seen it in the dropdown list, but not used it yet. If the Manual definition is corect (and it probably is) then I'd say your interpretation is right and your example should yield those results.
When B is not an integer, for instance 3.7, then the integer multiples of B are ....-3.7, 0, 3.7, 7.4, 11.1,.....But I do not know it rounds A down to one of those, or if the result is some integer...Again: this is not math, so who knows what it means ;)
It's probably something used in programming languages (like Modulo in Python,...), so a programmer will know how it works....
Well done!
Luckily, now that you understand it, you don't have to fill in all those numbers every time
Sometimes, when I don't understand what's going on, I start filling in a few easy ones, until I see the pattern.
Actually, that was due to the displacement.
Snapping works as explained above; here it snaps the X-value to integer multiples of -0.3:
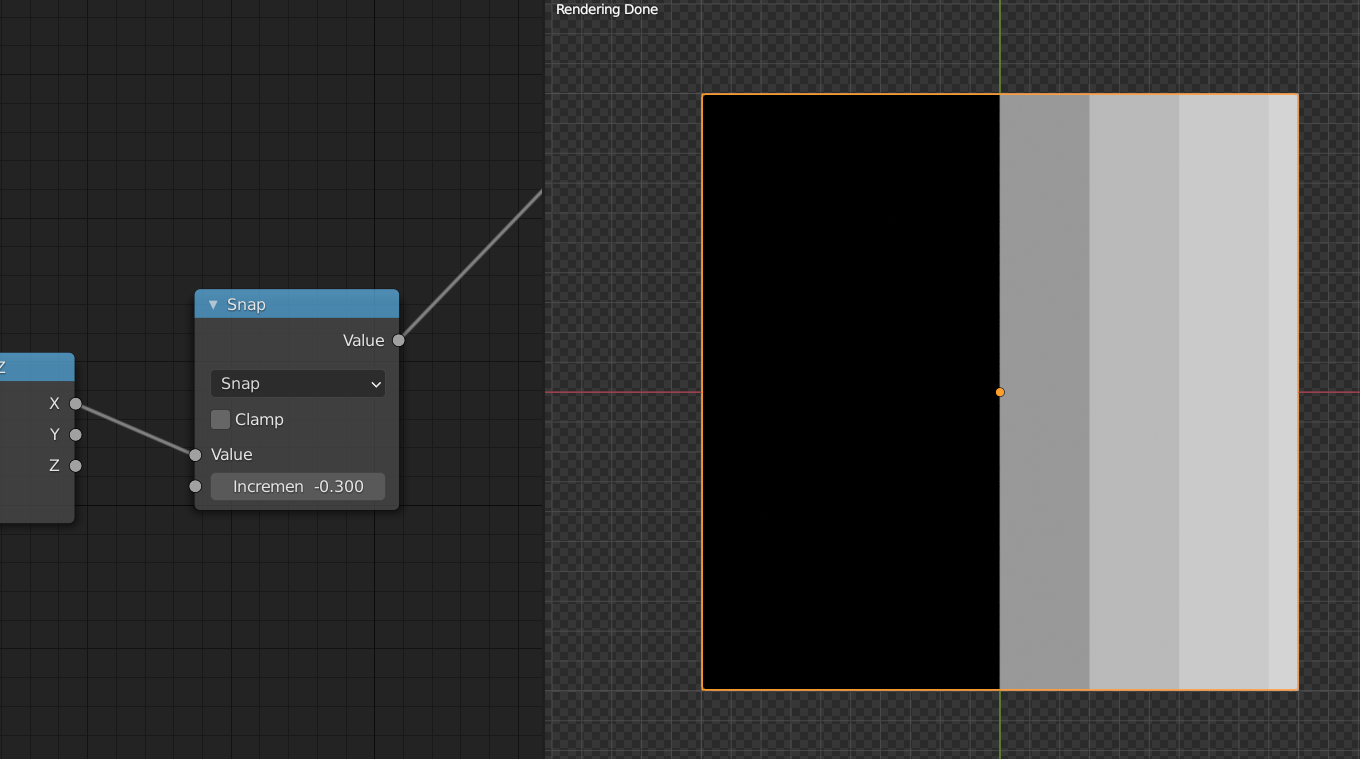
One day I'll understand all that stuff you guys are saying, one day soon.
Looking at this last screenshot again, I notice something's wrong, x=0.1 should Snap to 0, when increment is set to -0.3.
The integer multiples of 0.3 are the same as the integre multiples of -0.3, but the results of Snap are different:
????
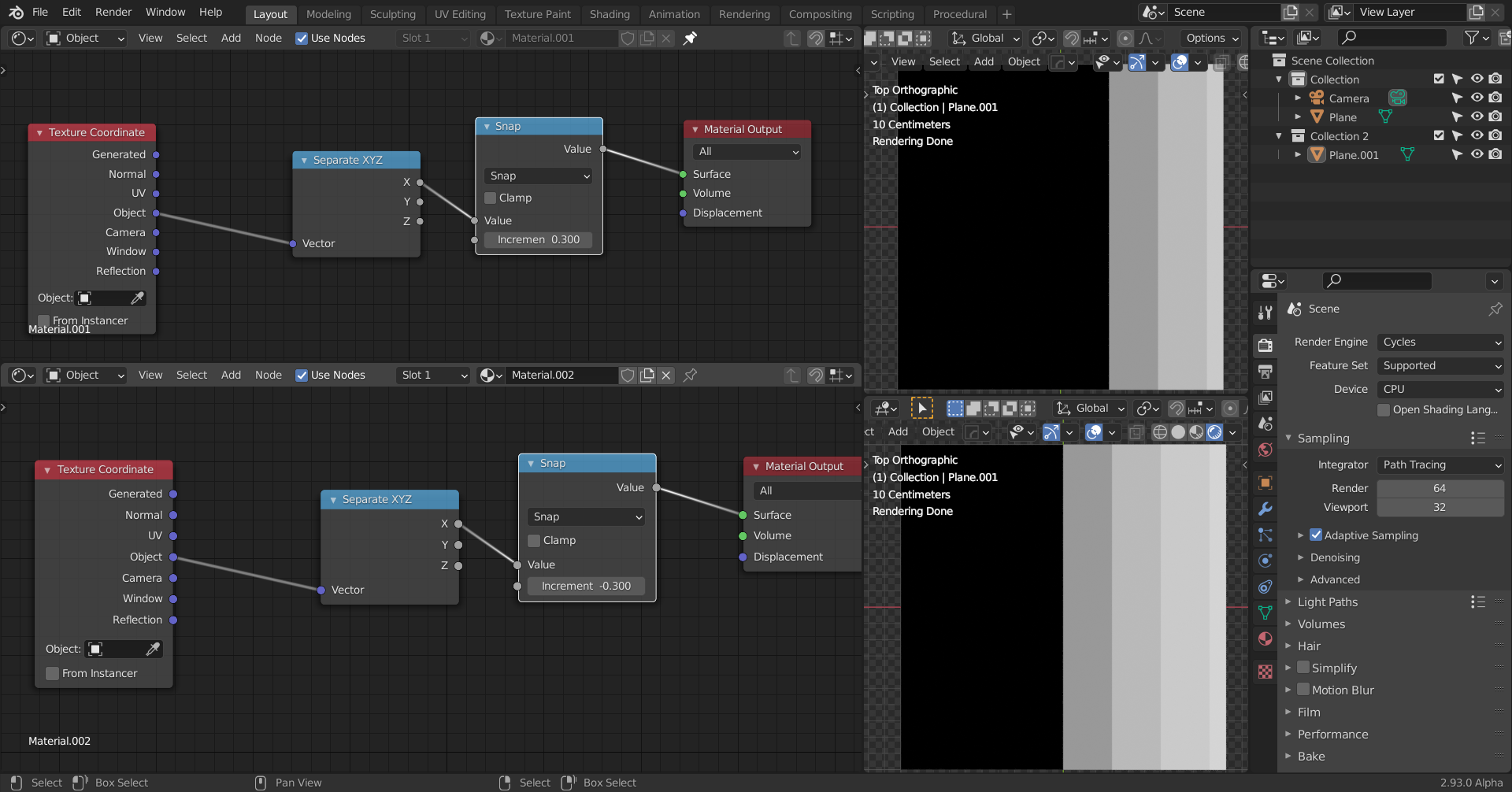
Key takeaways from watching 1. Fundamentals Chapter 1-1 Colors - Values - Vectors
- There are 2 things, colors and vectors, they can each be converted to values and values can be converted to colors.
- Color managements can influence how the color looks on screen, but that is a post effect, that does not influence the value.
- It is better to tun off Filmic and sRGB for debugging values.
- Colors are clamped from 0 to 1 but values can go negative numbers and beyond 1
- Going from a color to a value has downsides, since colors go by the luminosity, which is a perceived brightness.
- XYZ is interchangeable to RGB
