I'm wondering what is meant with "Shape Angle" in Blender's "Tris to Quads" operator. The official Blender 2.83 manual only mentions a "Max Angle":
Max Angle This value, between (0 to 180), controls the threshold for this tool to work on adjacent triangles. With a threshold of 0.0, it will only join adjacent triangles that form a perfect rectangle (i.e. right-angled triangles sharing their hypotenuses). Larger values are required for triangles with a shared edge that is small, relative to the size of the other edges of the triangles.
https://docs.blender.org/manual/ru/dev/modeling/meshes/editing/face/triangles_quads.html
The setting "Face Angle" obviously means the angle between the face normals.
I wanted to know this as well and since I couldn't find more info than you did I examined the code itself. Blender Github file
You are correct that the "Face Angle" parameter is compared with the dot product of the normal vectors of the two triangles (the angle between them).
if (delimit_data->do_angle_face) { if (dot_v3v3(f_a->no, f_b->no) < delimit_data->angle_face__cos) { goto fail; }}
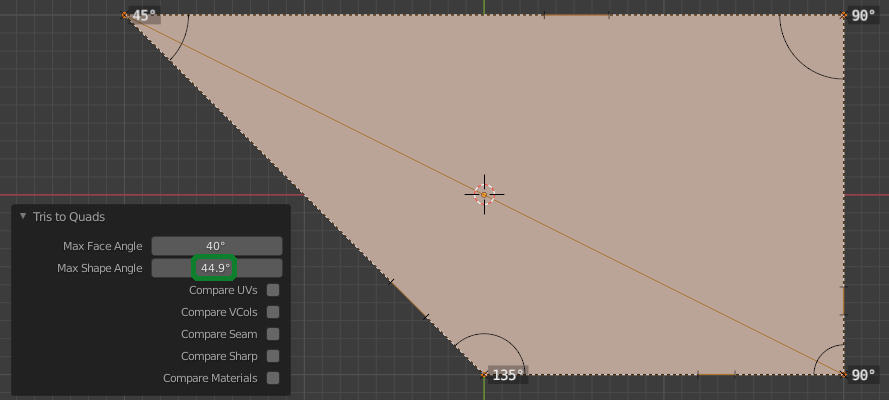
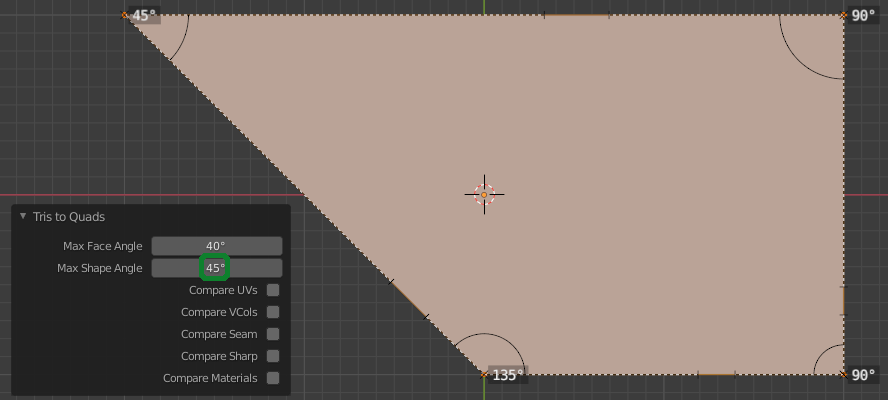
The "Angle Shape" parameter means, that two triangles are only merged into a quad if
|interior_angle - 90°| <= shape_angle
holds true for all 4 interior angles of the resulting quad.
The value is basically a measure for how much the resulting quad can differ from a rectangle.
(As the docs say: With a shape angle of 0°, only triangles are merged that form a rectangle)
This is the code (The condition is the inverse of the above because it's written as a fail condition):
if ((fabsf(angle_normalized_v3v3(edge_vecs[0], edge_vecs[1]) - (float)M_PI_2) > delimit_data->angle_shape) || (fabsf(angle_normalized_v3v3(edge_vecs[1], edge_vecs[2]) - (float)M_PI_2) > delimit_data->angle_shape) || (fabsf(angle_normalized_v3v3(edge_vecs[2], edge_vecs[3]) - (float)M_PI_2) > delimit_data->angle_shape) || (fabsf(angle_normalized_v3v3(edge_vecs[3], edge_vecs[0]) - (float)M_PI_2) > delimit_data->angle_shape)) { goto fail; }
Two more pictures to illustrate this:
Thank you very much, ffabianm , for this profound explanation! Excellent👍🏆!