I would like to create a model for printing with 0.4 mm resolution that is a hollow, bottomless rectangle with chamfered corners. (Like the top of an Altoids box.)
I am using a very manual process to get sufficient resolution in the mesh because of the angle of the quads at the corners, and I'm still not getting quads everywhere.
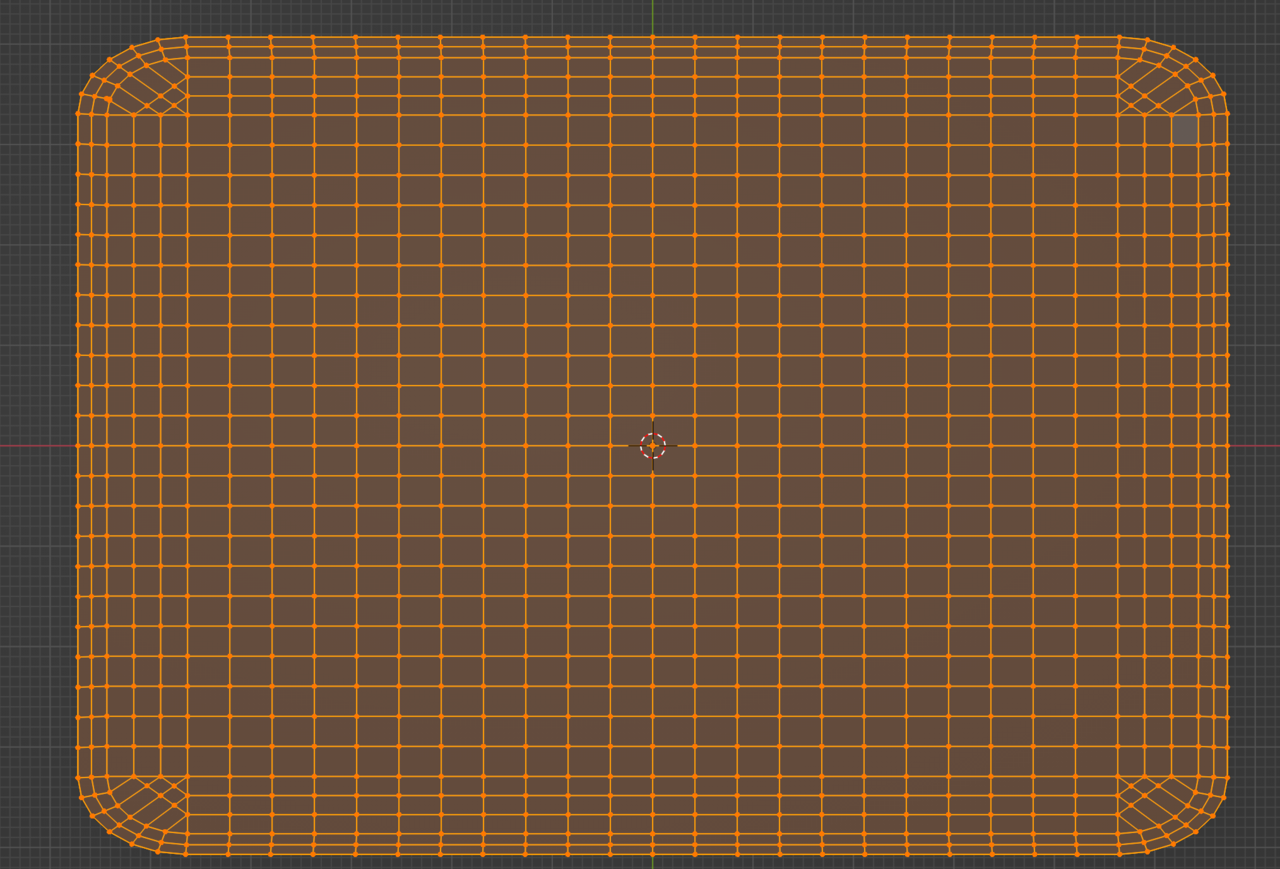
Is there a way to create high(er) resolution without getting very long triangles because of the corners? I've had to manually draw in lines as well as do partial selections to subdivide.
Totally the contrary, 3D printing is very forgiving with the mesh and triangles, Ngons and all of it, you can have a mess of a model and it doesn't really matter that much. You can watch the 3D printing course and see how Porter does it:
https://cgcookie.com/courses/make-it-3d-printing-with-blender
Thanks for the solution. I was trying something like that but now, after seeing what you've done, I realized that the number of inset loops matters to make the topology work out properly.
Part of the problem with subdividing the way that I have been trying is that some regions end up with absurdly high resolution, and other sections have much lower resolution.
I watched a big chunk of the printing course, and tried to apply bezier curves, but that was much harder than I anticipated. I don't quite understand how to get a closed curve that isn't janky, and this is a symmetrical application, so I was trying bevels to begin with.
Thanks for the help!