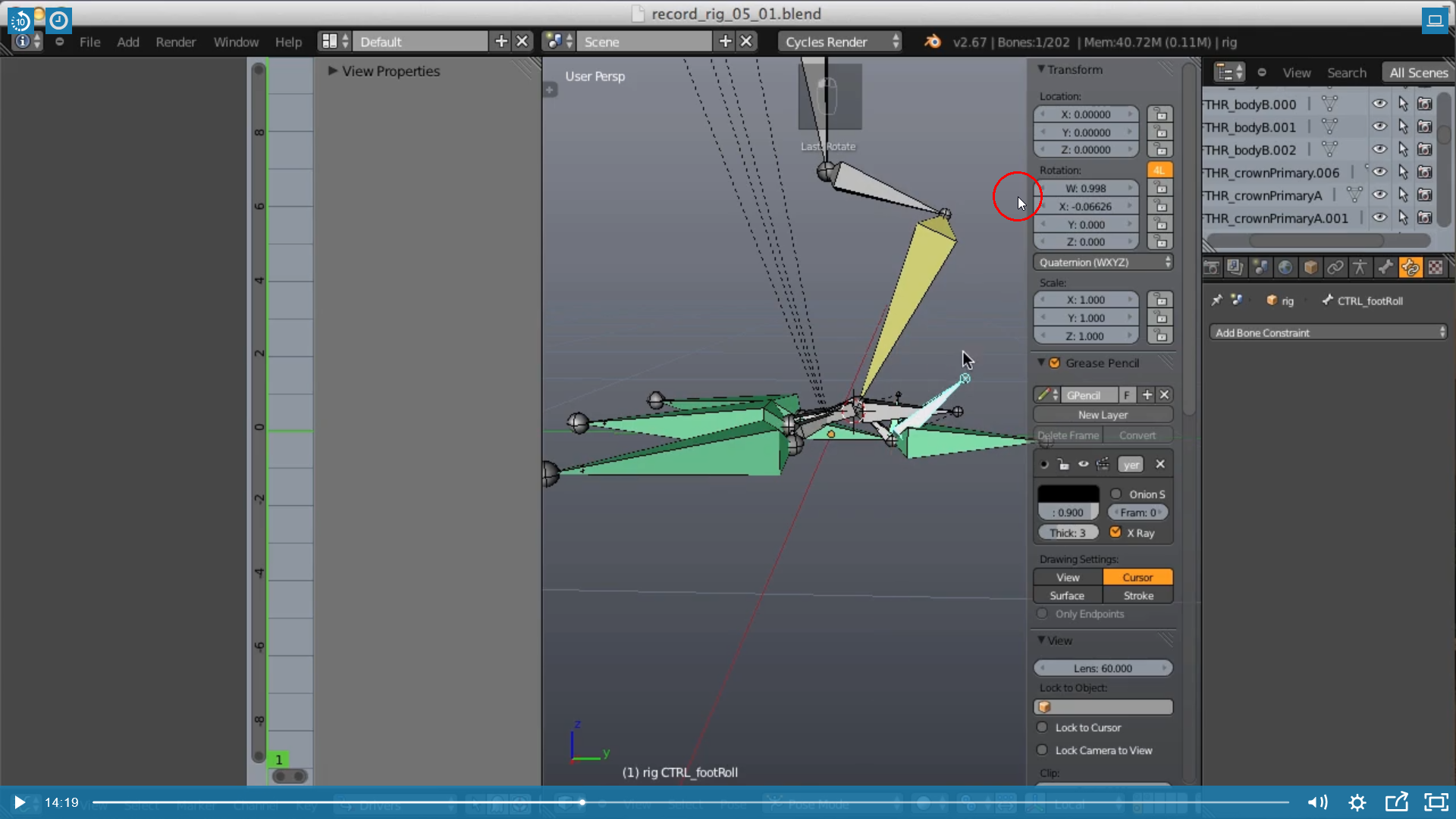
I'wondering why an "X Rotation" value of "-0.06626" of the "CTRL_footRoll" bone is translated into a "Scripted Expression" value of "0.133" with "-var" as "Scripted Expression":
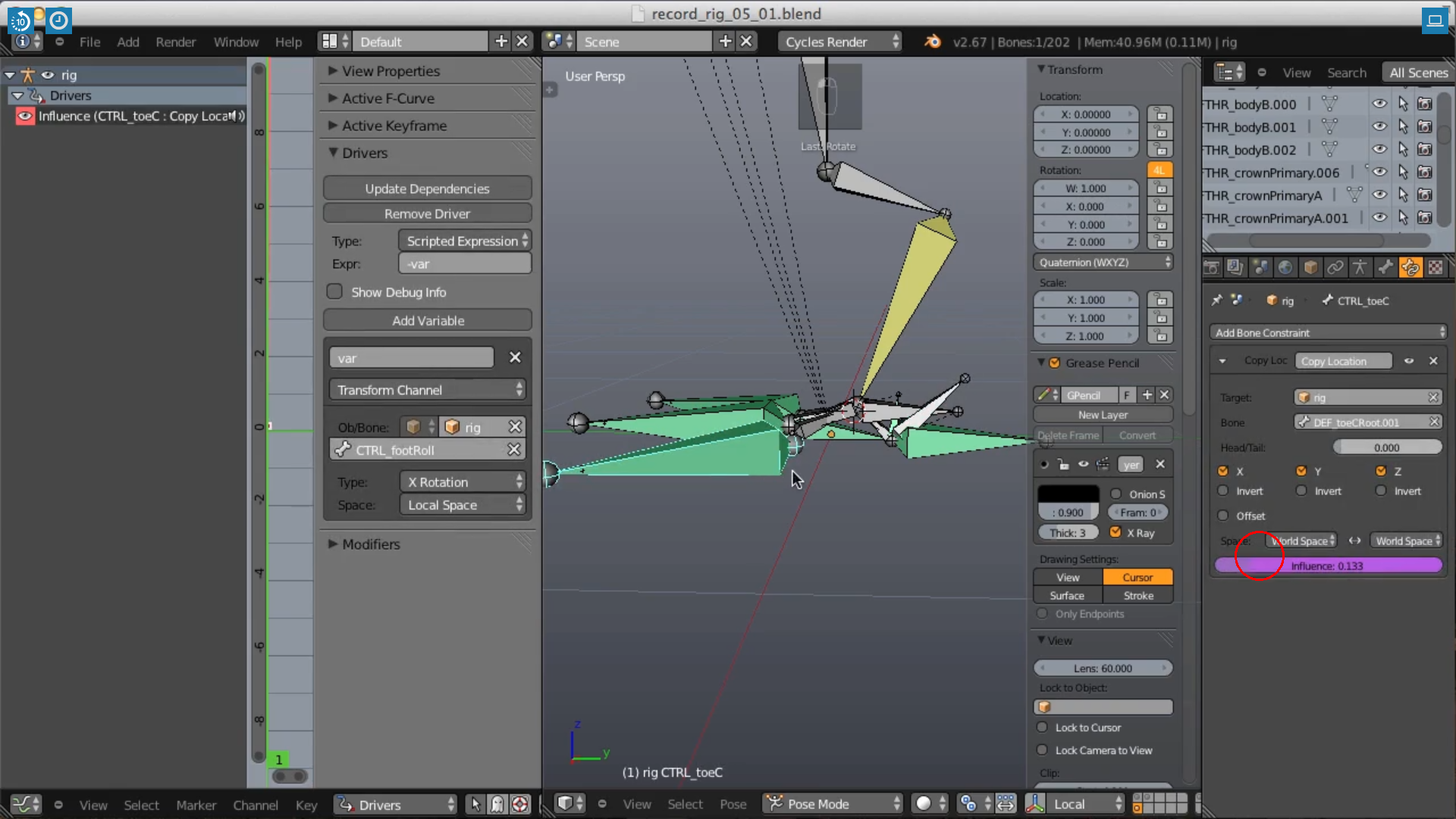
At 15:44 and the following seconds in the video "Rotation X" is set to 0.28" and "var" as the only "Driver Variable" copies the "Local Space X Rotation". Therefore, I expect the expression "-var +1" to have the value of "0.72", but it's "0.433" that is beeing fed into the driven "Influence" value!
I've just seen that in Blender 2.90 you can select a "Mode for calculating rotation channel values" which is set to "Auto Euler" per default:
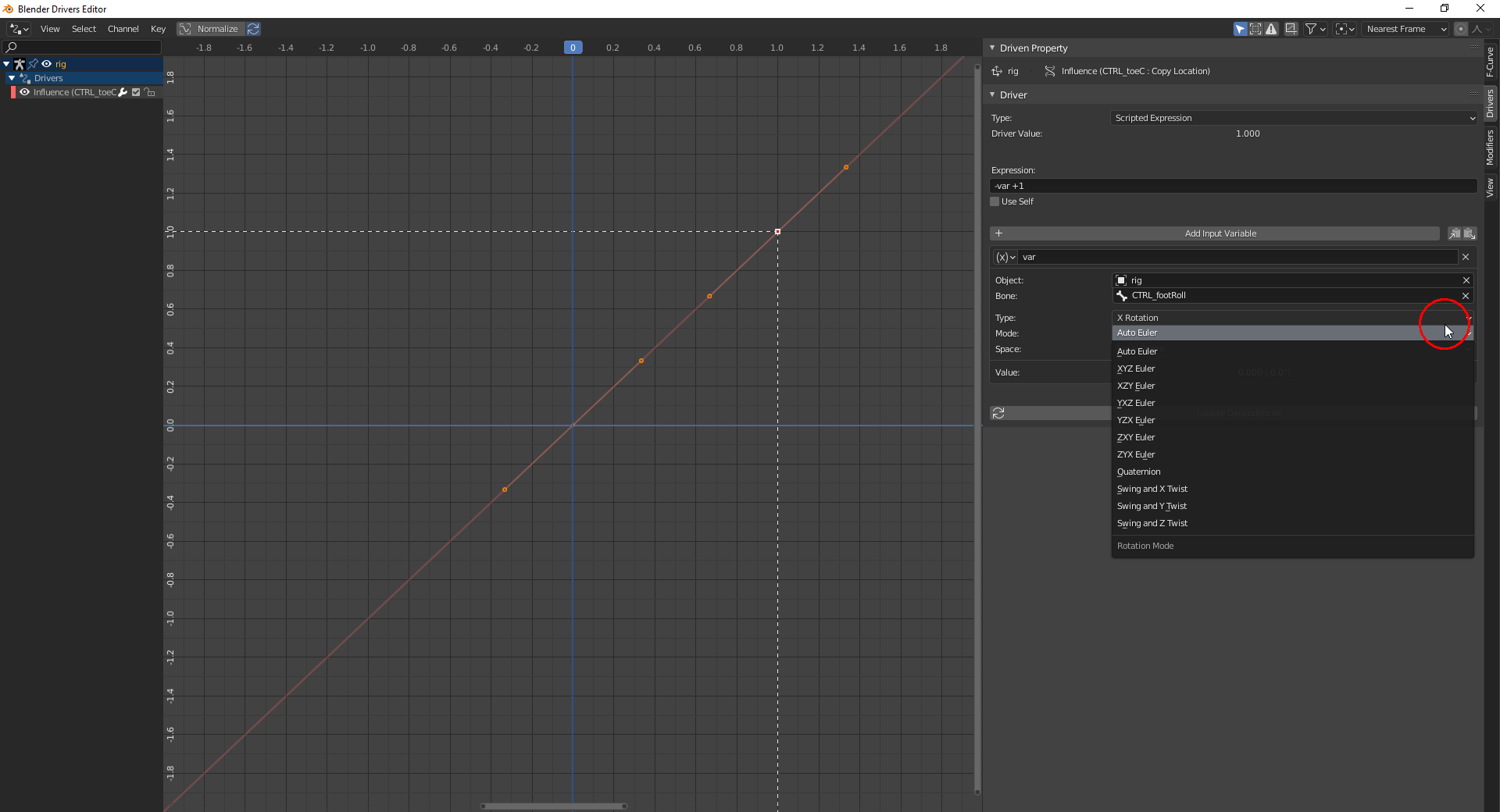
Since the "Bone Rotation" in "Pose Mode" is set to "Quaternion" per default, one might suppose that this could be the explanation for the discrepancy described above. Blender 2.67, which is used by Kent in the video, doesn't offer that "Mode Selection".
I've just read in the "Blender Manual" here that the values for X, Y and Z within the "Quaternion Rotations" define a "Rotation Axis" and W a "Rotation Angle" around that axis. But setting it to "Euler Rotations" can lead to a "Gimbal Lock".
Rotate a bone in "Quaternion (WXYZ)" (default for bones in "Pose Mode") around its "Local X Axis" and "W" as well as "X" will change!
...the values for X, Y and Z within the "Quaternion Rotations" define a "Rotation Axis" and W a "Rotation Angle" around that axis
This is not correct! The rotation angle is 'hidden' in all 4 variables W, X, Y and Z.
If the vector for the axis of rotation is (x, y, z), then:
W = cos(angle/2)
X = x*sin(angle/2)
Y = y*sin(angle/2)
Z = z*sin(angle/2).
It should be clear from this that you cannot change only one variable without affecting at least one of the other three...
You could say that a quaternion is a 4 dimensional vector of length 1!
Somebody should actually explain quaternions in a clear and understandable way here ;)
Thank you, ![]() spikeyxxx, you already brought light into the darkness😀!
spikeyxxx, you already brought light into the darkness😀!
For "Quaternions" in Blender, there's also a good article in the "Blender Art Magazine" with the title "A world of rotations" here. On page 16, the author writes that "W" is the "Rotation Angle" around the axis defined by "X", "Y" and "Z".
But your explanation, ![]() spikeyxxx, is obviously the correct one since this is the most precise definition for "X", "Y", "Z" and "W" 👍! I think, part of the confusion is that we also have "X", "Y", "Z" and "W" in "Axis Angle Rotation".
spikeyxxx, is obviously the correct one since this is the most precise definition for "X", "Y", "Z" and "W" 👍! I think, part of the confusion is that we also have "X", "Y", "Z" and "W" in "Axis Angle Rotation".
Which "Scripted Expression" do I need so that I can use the rotation of a bone around its "Local X Axis" in a driver if the coordinate system is set to "Quaternion (WXYZ)" ?
The mentioned article does have some, what I would call massive mistakes in it..it seems to me that the writer has had it explained to him and he didn't completely understand it.
I think, part of the confusion is that we also have "X", "Y", "Z" and "W" in "Axis Angle Rotation"
That is indeed very confusing! Those are completely different things!
Unfortunately, I don't understand the rig and what exactly needs to be driven by what...and using Local Space doesn't make it easier for me.
To be precise:a quaternion is a number(!) and the W is the real part of that number and the X, Y and Z are the imaginary parts.
So nothing to do with X, Y and Z axes.
Just as an illustration for the advantages of "Quaternion Rotation" compared to "Euler Rotations" when dealing with rotations around all three axes:
1) XYZ EULER: Rotating Suzanne around the "Local Y Axis" 90 degrees causes "Gimbal Lock" (the inner "X Axis" gets aligned with the outer "Z Axis" so that we effectively loose X as "Rotation Axis") which Blender has to solve by a slight detour when turning Suzanne to the front:
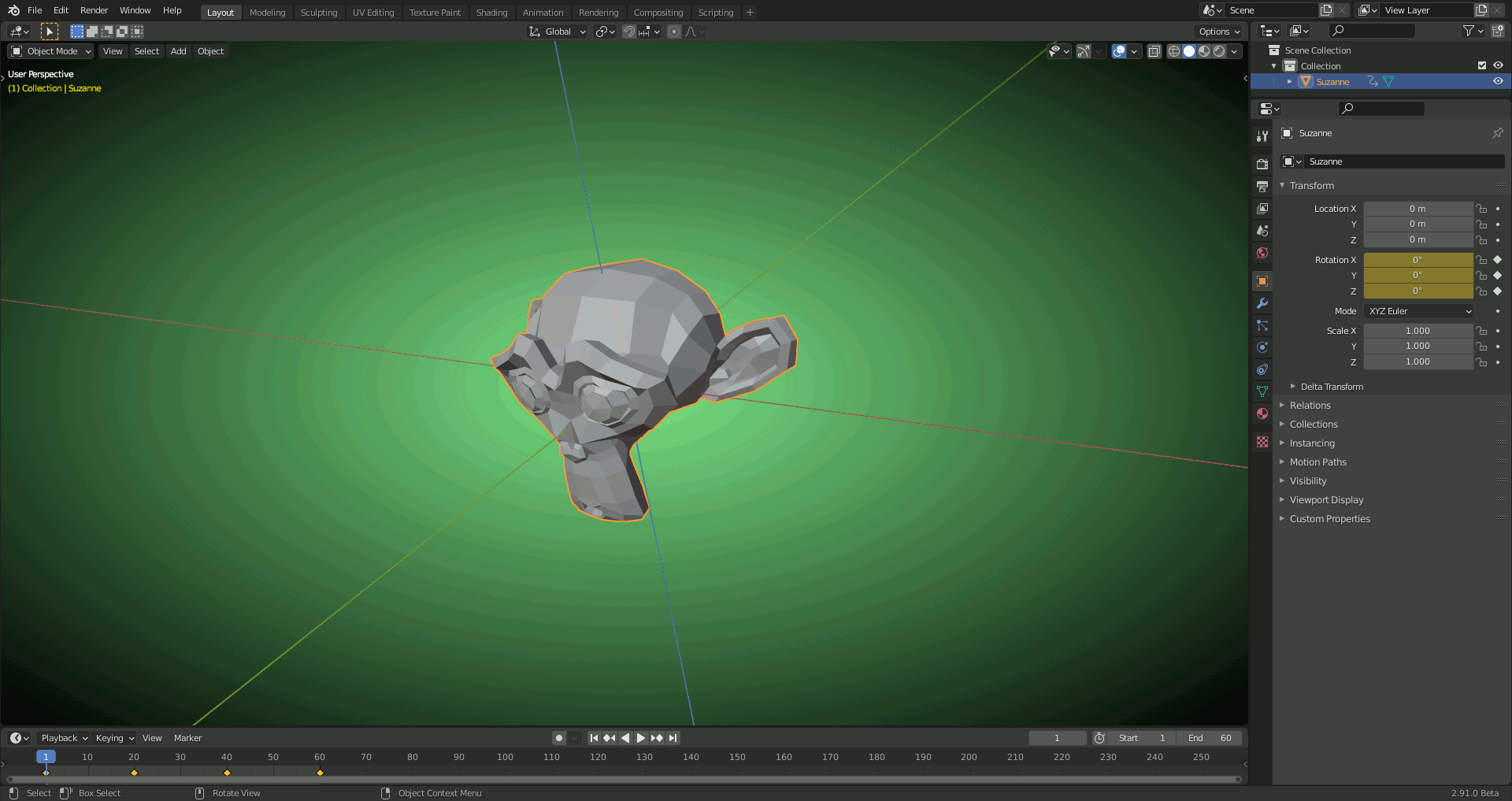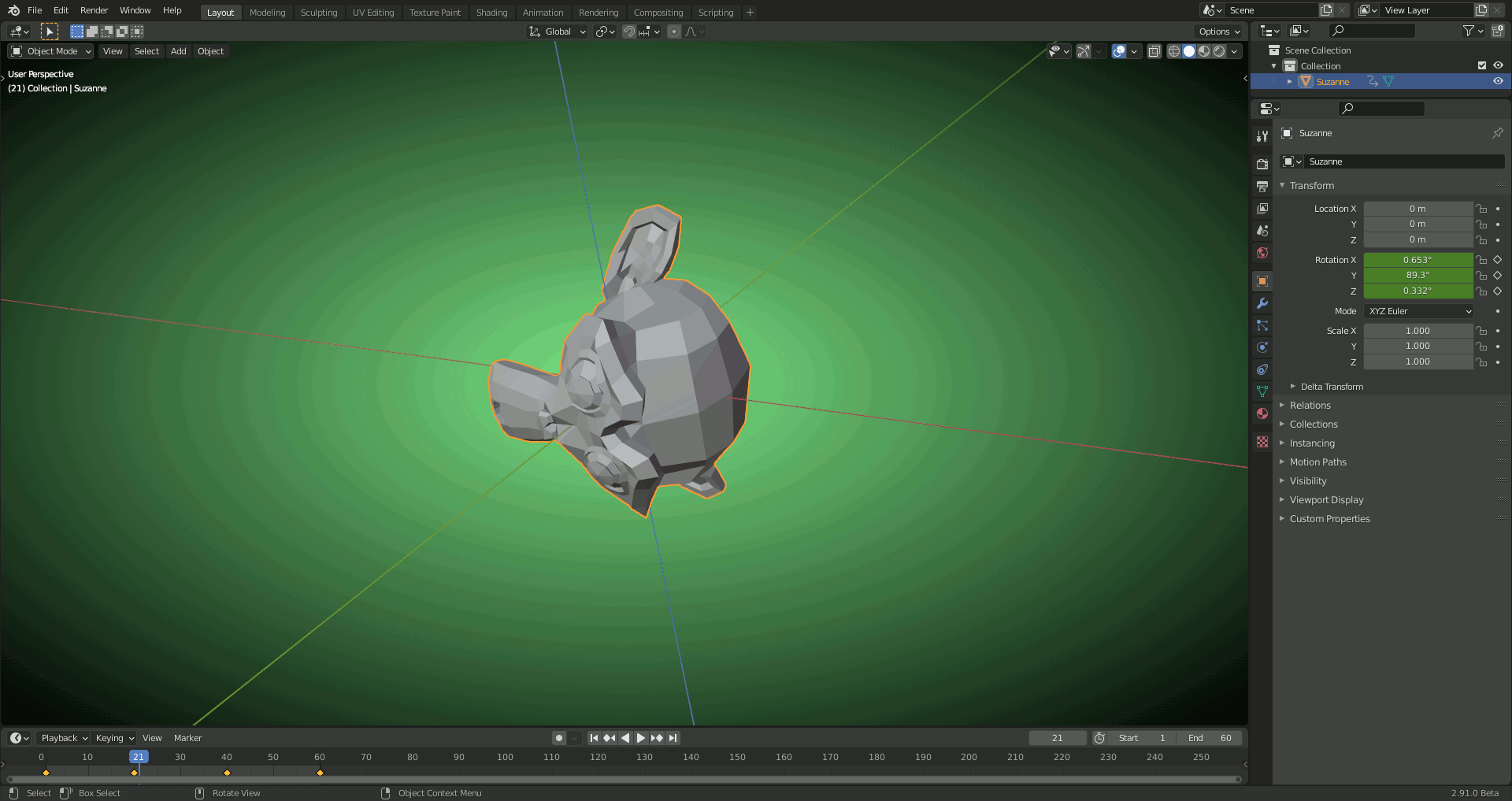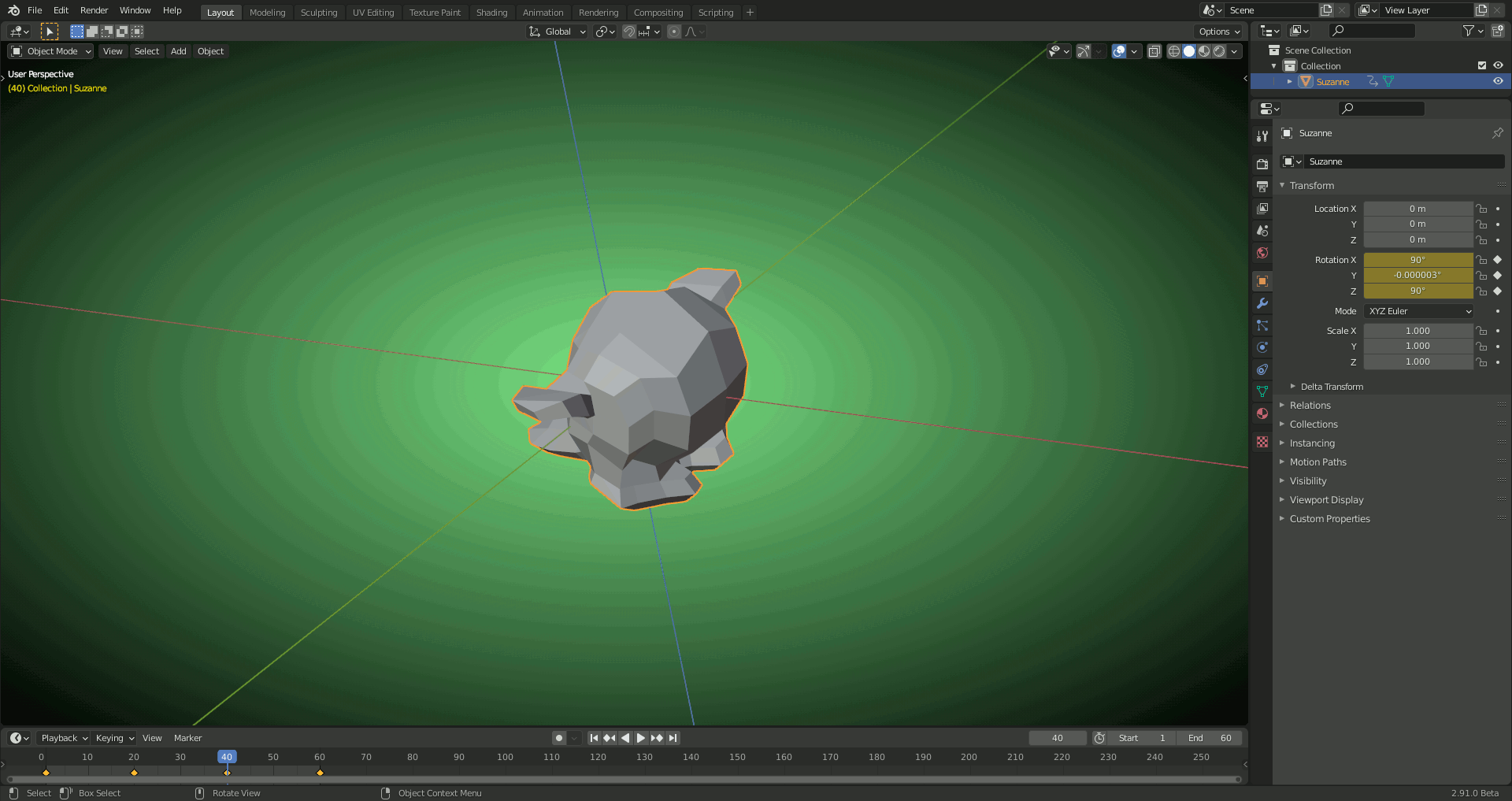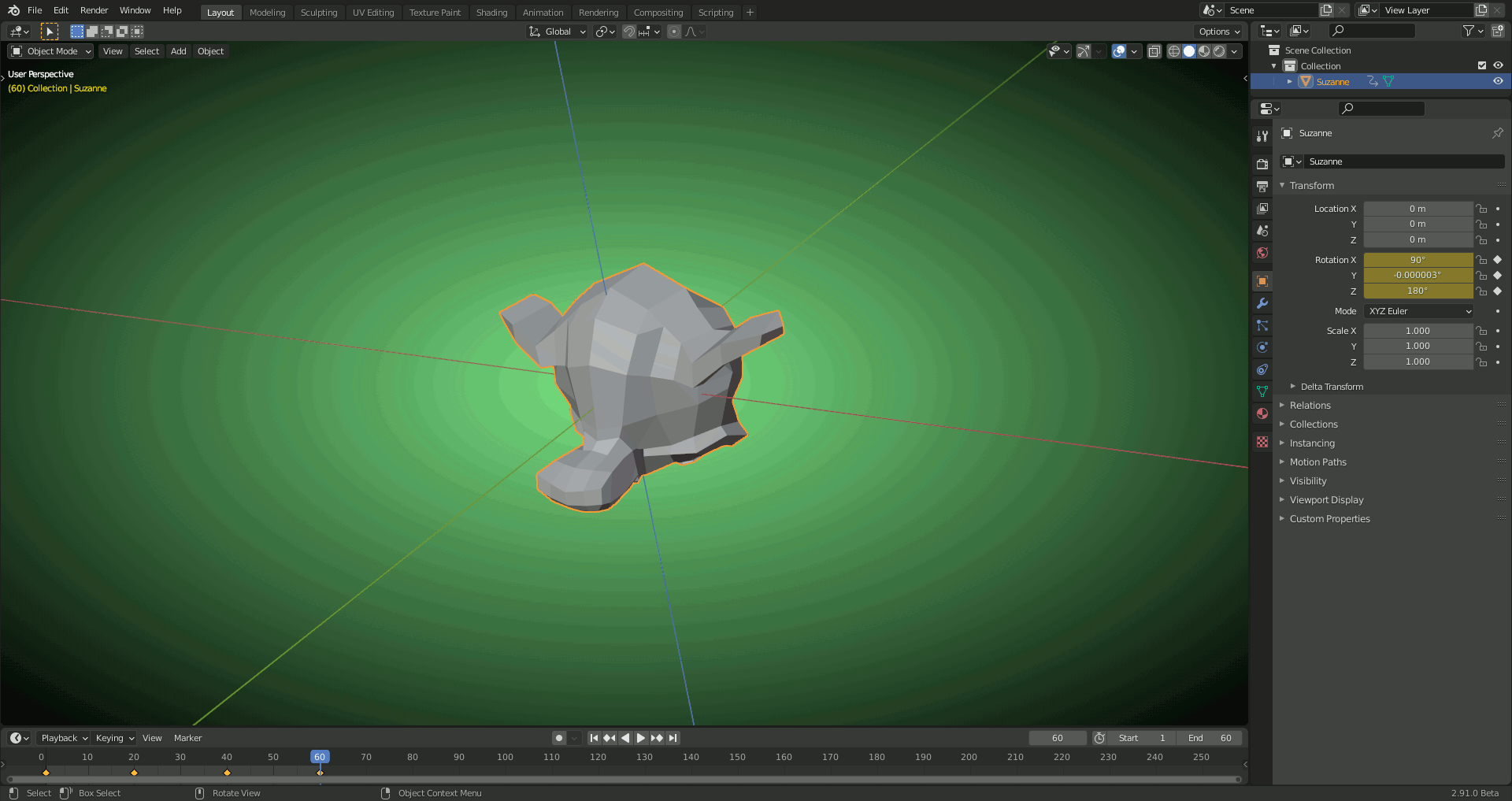
2) With QUATERNION: Smooth blending between the keyframes (no detours):
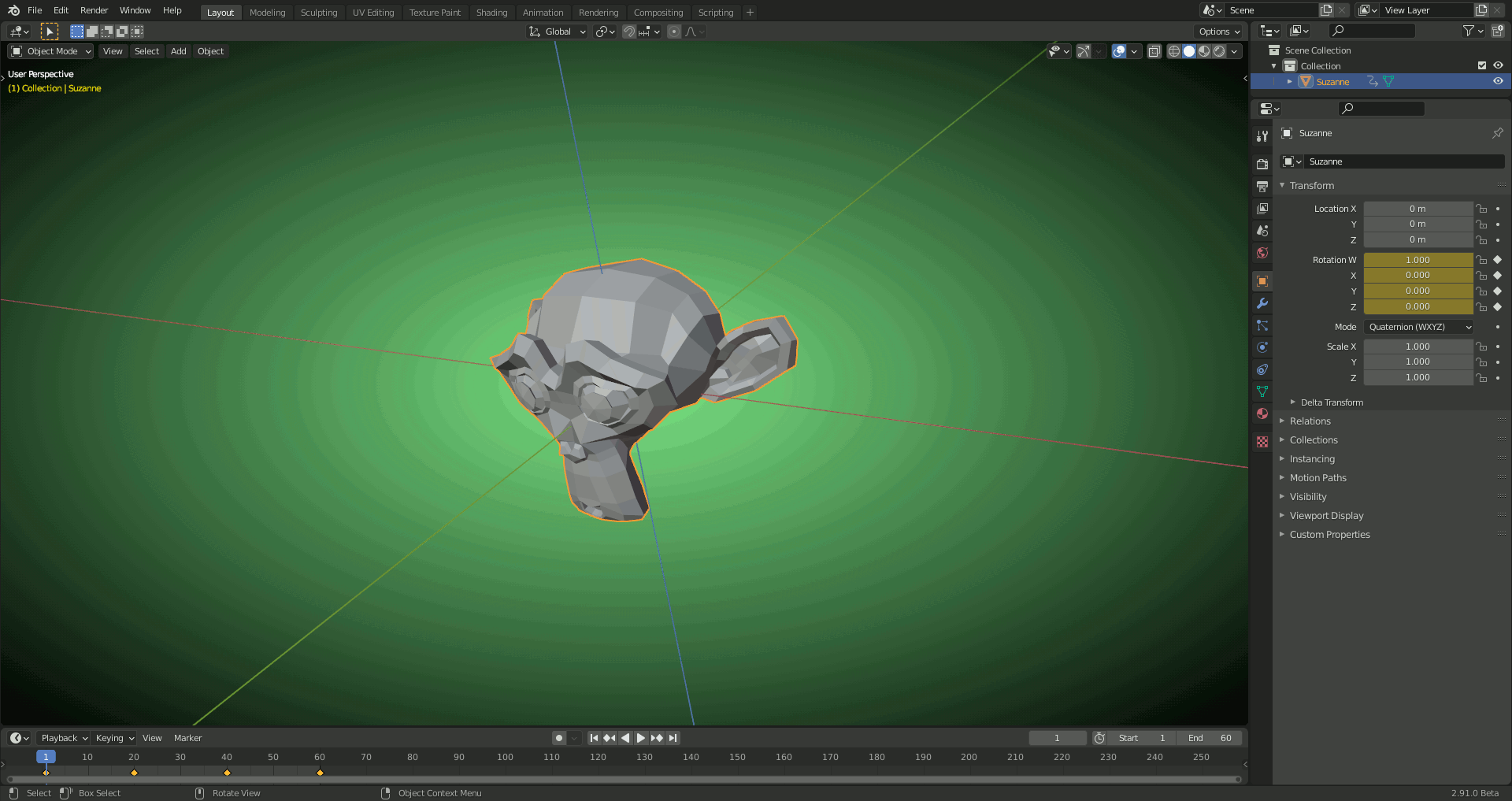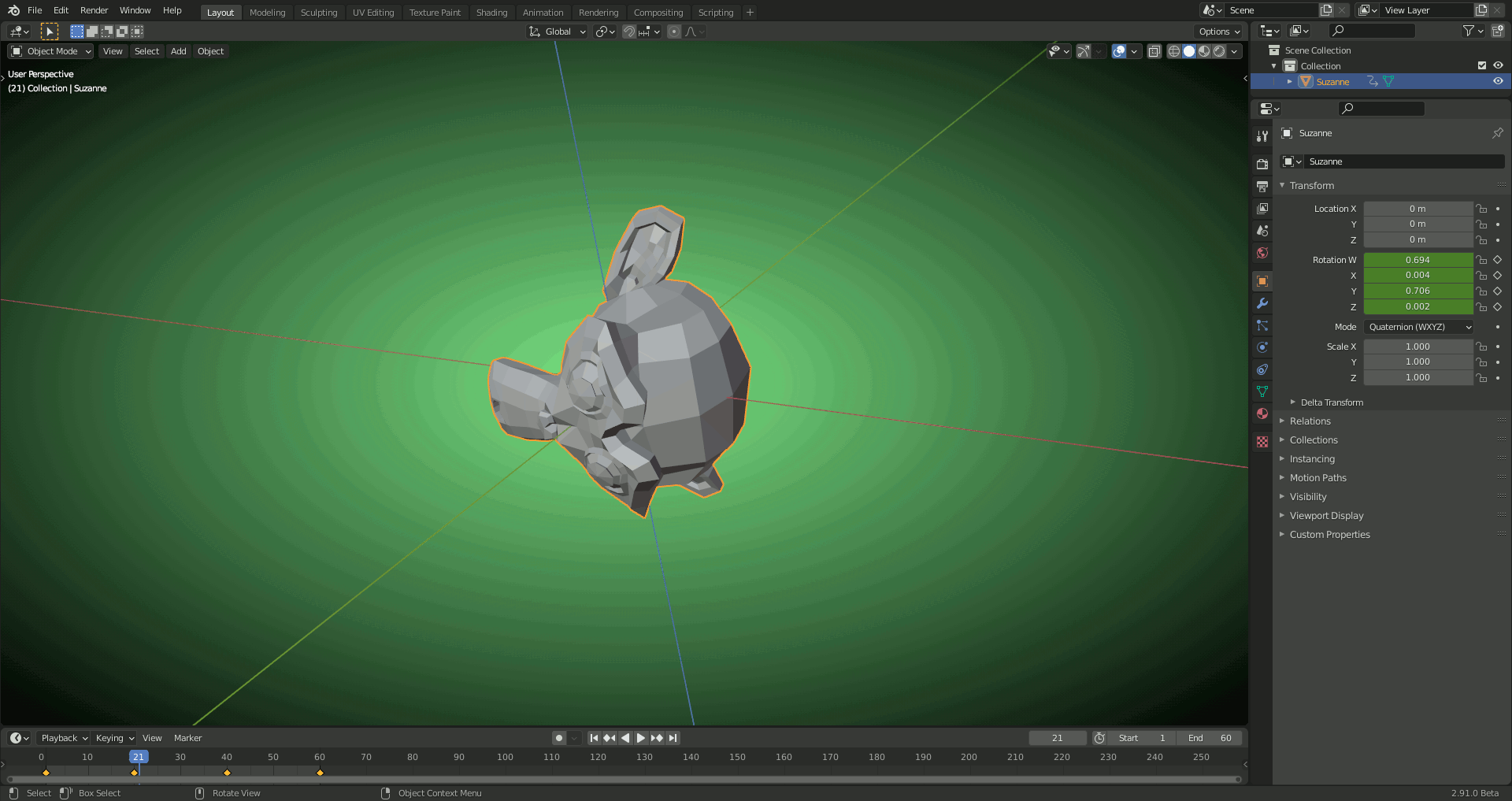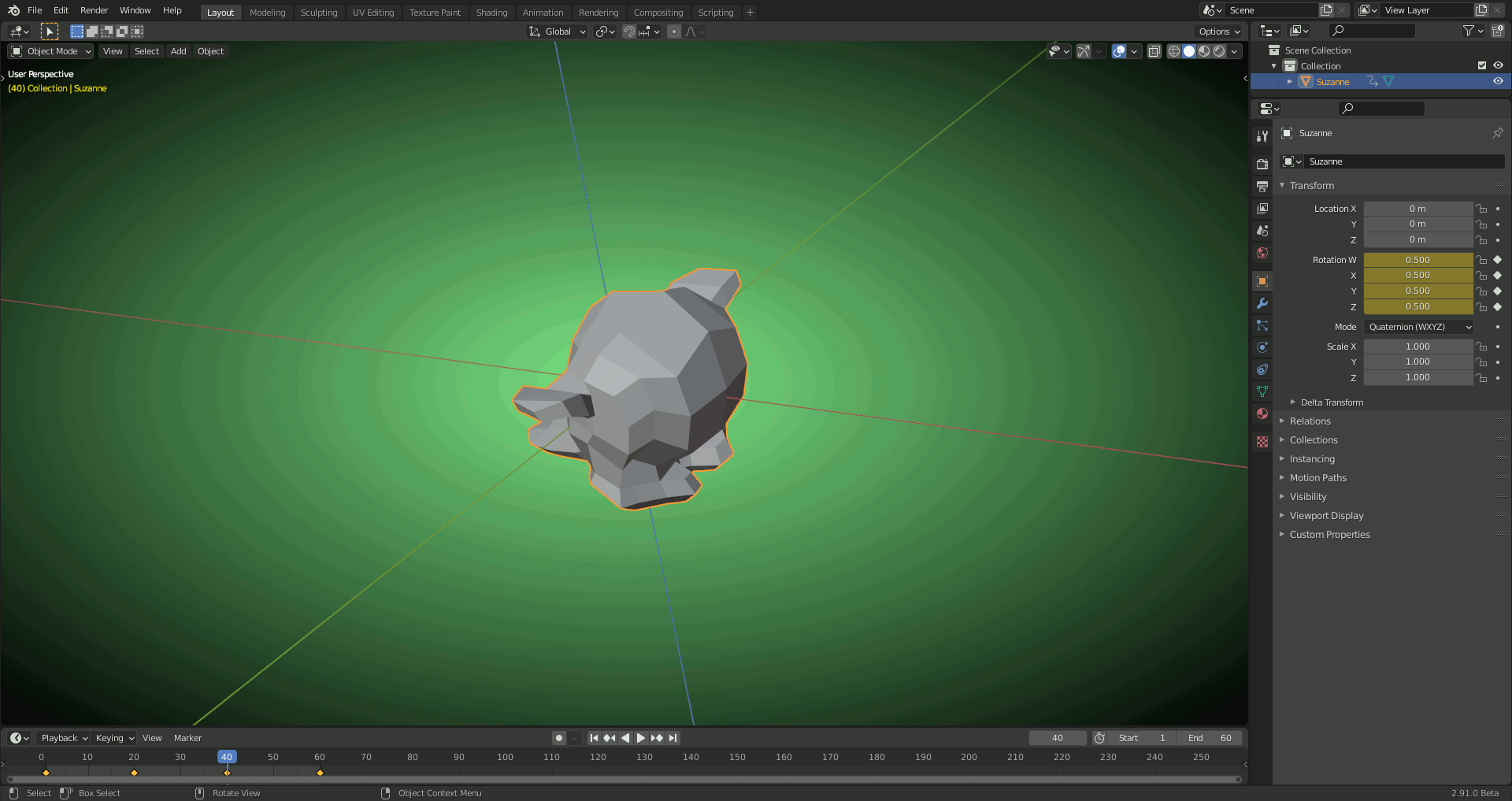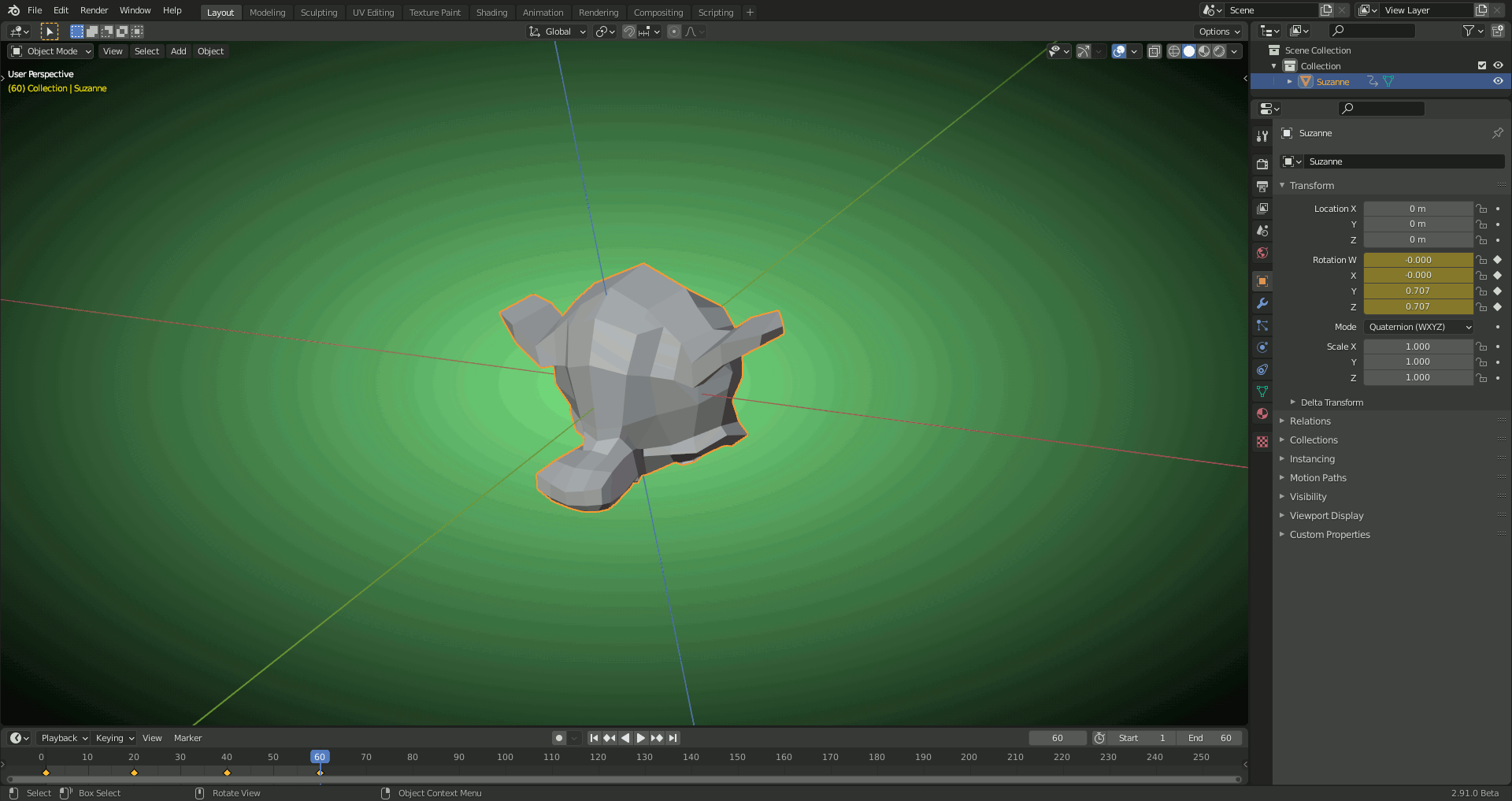
Note: The keyframes are linked to the different "Rotation Coordinate Systems" so that the different animations can easily be selected by switching between both systems.
The "Control Bone" "CTRL_footRoll" shall during its rotation to the front toes set the "Influence" of the "Copy Location Constraint" on "CTRL_toeC" set to "0" so that this bone stays on the ground instead of moving slightly upwards (see video from 11:59 on):
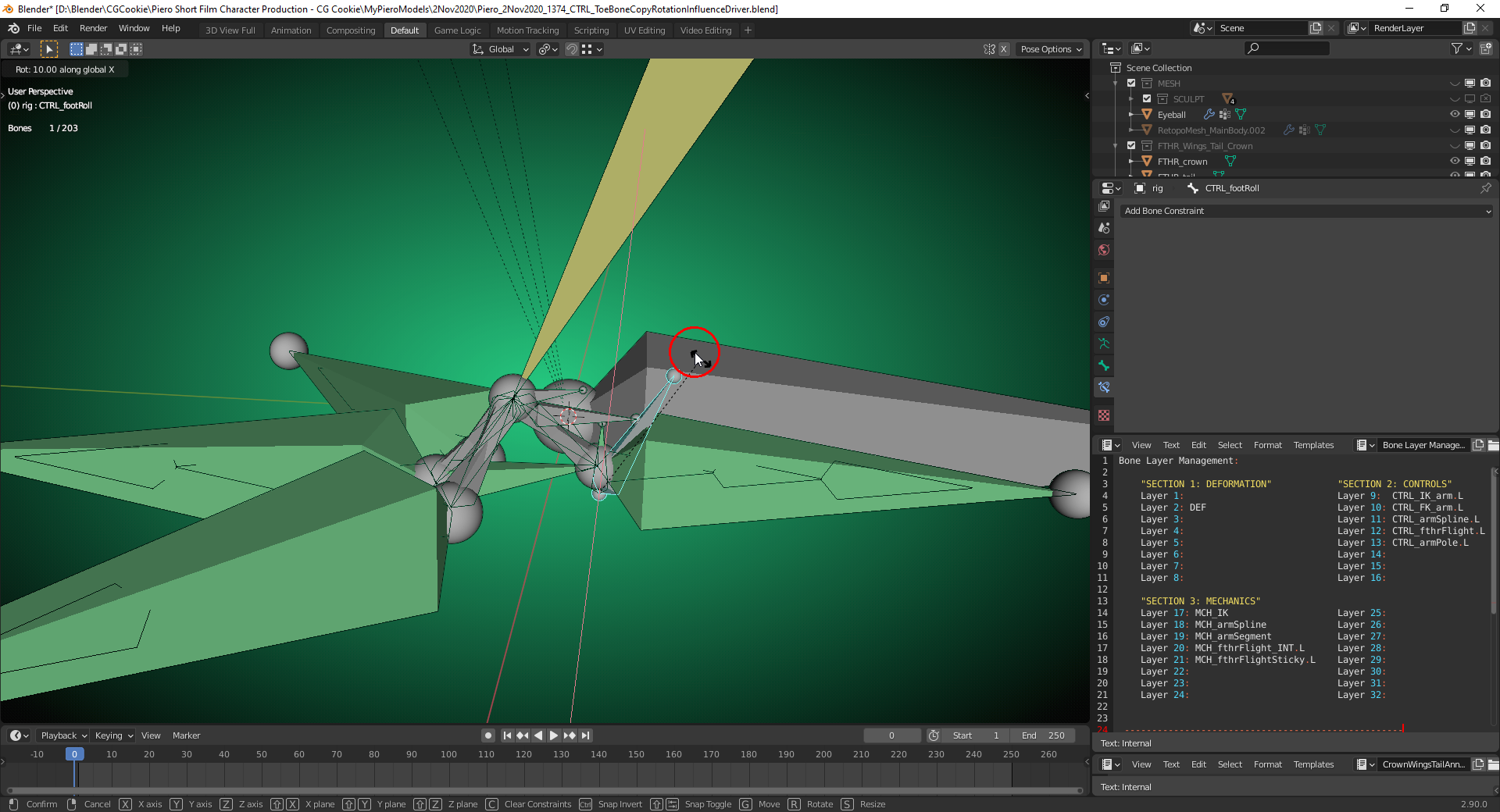
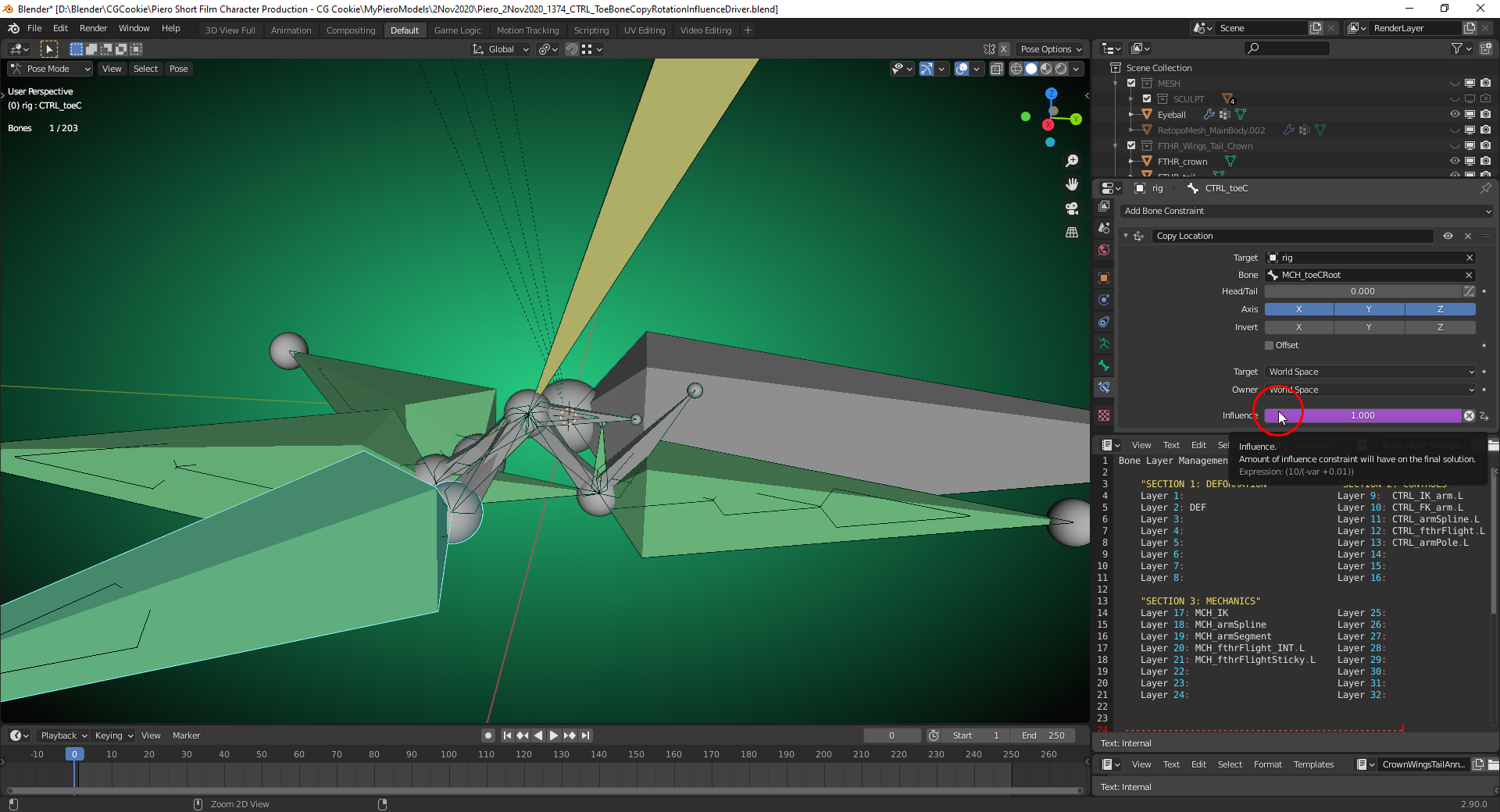
When rolling "CTRL_footRoll" backwards the "Influence" of that shall be reset to "1" again in order to make the "CTRL_toeC move upwards.
The rig is here.
Hi ![]() duerer , I didn't read the whole article you mentioned but it seems the author states that the 4d vector is 'like' axis angle.
duerer , I didn't read the whole article you mentioned but it seems the author states that the 4d vector is 'like' axis angle.
Listen to ![]() spikeyxxx when it comes to Quaternions. He knows what he's talk about ;)
spikeyxxx when it comes to Quaternions. He knows what he's talk about ;)
Here's a simple way to think about them.
If something only rotates on 1 axis. Use Euler.
If something has to rotate on all 3 axes. Use Quaternions. This will save you from any Gimbal lock issues.
As per the drivers in the tutorial, I think it's actually easier and more straight forward to use a 'transform constraint' and a 'limit rotation constraint' rather than the way shown in lesson, however, this requires a little bit of a different setup from what is shown in the course. So I would actually stick to what is shown rather than trying to go rogue haha.
There is always more than 1 way of doing things in 3D ;)
Thanks, @waylow, setting up such a complex rig is really tricky. If you "turn a screw" in one place, things change in another place and this maybe not as you intended it. So, you try to fix it there and change the rig's behaviour in yet another place ... There's a lot of back and forth jumping which can easily lead to confusion. I admire everybody who successfullly sets up a complex rig without becoming insane 😉! Kent's "Piero Rig" and Stan Paillereau's "Book Rig" are really awesome👍👍👍!!!
When it comes to "Quaternions", the explanations by ![]() spikeyxxx are by far the best and most precise! So, I'm using them as orientation. In the "Humane Rigging Course" (now in the Blender Cloud), the author gives an intuitive model for animations with "Quaternions" comparing their use with color mixing. But using this in practice doesn't seem to me as easy as it sounds since even with a rotation around only one axis at a time, there're two values changing, "W" and either "X", "Y" or "Z".
spikeyxxx are by far the best and most precise! So, I'm using them as orientation. In the "Humane Rigging Course" (now in the Blender Cloud), the author gives an intuitive model for animations with "Quaternions" comparing their use with color mixing. But using this in practice doesn't seem to me as easy as it sounds since even with a rotation around only one axis at a time, there're two values changing, "W" and either "X", "Y" or "Z".
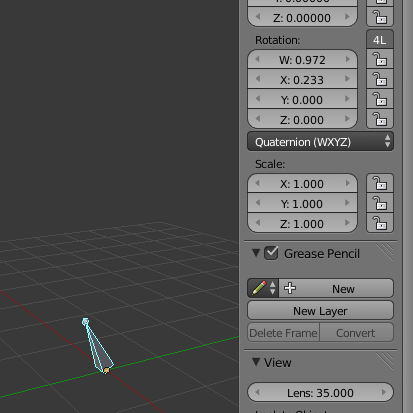
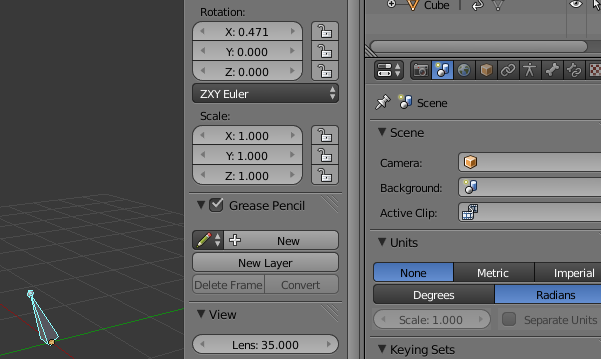
Using "Quaternions" in older Blender versions can lead to wrong values within "Drivers". A "Quaternion Rotation" in Blender 2.66 with "X = 0.233" results in the value "0.263" when using it in a "Single Variable Expression" in a "Driver" as can be seen here. with a bone's "X Rotation" driving the "Z Location" of a cube. Blender 2.90 can handle "Quaternion Rotations" properly since you can also select "W Rotation" as driving value which wasn't possible in Blender 2.66.
Seems to be working in 2.66a, when not using a constant in the scripted expression field:

and of course using Euler for the bone and radians: