@theluthier It's totally okay to make a circle with 7 vertices around each nostril since seven is the number of perfection 👍😀!
I didn't know that. Why is seven the number of perfection duerer ?
I know that 6 is a perfect number (it equals the sum of its 'real' divisors: 1+2+3), and that every natural number under 10 is magicall (see religions, fairytales, etc), but this is new to me; never too old to learn something new...
spikeyxxx It's a theological interpretation, not a mathematical one.
A.
According to the Bible, God created the world in six days and sanctified it only through the seventh day (see Genesis 2: 2-3; see also Exodus 20: 8-11; 34: 21). So, six stands for the material perfection without God's mercy and seven stands for the perfection of the human work with God's mercy.
B.
The resurrection of Jesus is the seventh in the Bible after the following six:
1) The prophet Elijah resurrected the son of a widdow in Sarepta by spreading his arms three times over the boy. (First Book of Kings 17: 21)
2) The prohet Elisha resurrected the son of a noble lady in Schunem by lying down on him. The boy sneezed seven times before opening his eyes. (Second Book of Kings 4: 35)
3) After the death of the prohet Elisha during a sudden attack of troups from Moab, a dead was carried to his grave but when the people saw one of these troups they threw his body into Elisha's grave where the dead touched Elisha and began to live again. (Second Book of Kings 13: 21)
4) Jesus Christ resurrected the daughter of the synagogue leader Jairus (see the Gospels according to Matthew 9: 25, Mark 5: 41-42 and Luke 8: 54-55)
5) Jesus Christ resurrected the only son of the widdow from Nain, when he was carried to his grave (see the Gospel according to Luke 7: 14-15)
6) Jesus Christ called the Lazarus who was already dead for four days to leave his grave (see the Gospel according to John 11: 43-44)
I know that its not a mathematical interpretation, of course ;)
And I am not a religious person, but if I remember correctly every number below ten is a holy number and I do not understand why (only) seven is (more) perfect (than others), because of my lack of religious knowledge.
I think two reasons are not a lot, but I'm sure there are more.Anyway, I'll gladly take your word for it! Thanks.
spikeyxxx there're certainly countless interpretations in many cultures and religions about the meaning of numbers. The one I've written about certainly had a major cultural impact due to the wide spread of the jewish and christian religion in the world. The seven day scheme is directly at the beginning of the Bible giving a theological interpretation of the world so that it has a special position. The list for the seven as the number of perfection can be extendend further ... but not here 😉
But I've a reason for the seven as the number of perfection that no doubt beats them all: I'm born on a seventh 😉😁!
7 seems to be associated with temples in the ancient near east. Baal’s temple was built in 7 days and Enuma Elish (a Babylonian temple text) was presumably read during the 7 day New Year festival. There is a 7 stage structure to the building of the tabernacle in Exodus. Interestingly, I think Genesis 1 is a critique against the temple system as it existed under the monarchy (and the monarchy in general) and thus features a similar 7-fold structure.
The 7 resurrections strikes me as “theologian math” as one is unique to Luke and one unique to John, though I can definitely see John throwing it in with the express purpose of lining up the numbers.
And yes, you can go to the Norse for nines and further East for threes and fours. And probably elsewhere for the rest, but it is all very interesting to be sure. I think the running theory on why sevens were significant was the ancient fascination with the seven celestial bodies (the ones visible to the unaided eye) that move through our sky.
Thank, pprocyonlotor, for your explanations 😀! The last one especially pleases me as amateur astronomer 🔭🌞🌕🪐🌌!
There're also the seven main colors in a rainbow 🌈 (see e.g. here) and in music a scale has seven tones 🎶.
for spikeyxxx
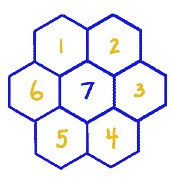
consider the word "perfect" as "complete" and this begins to explain the relevance of 7 in the religious realm...
Interesting 🤔
(I have a great difficulty disconnecting numbers with math, personally...)
So, what do we have here? A hexagon, with (obviously) 6 sides? So we assign the number 7 to the hexagon?
(If you say 7, I think:" 7 is a prime and 7-1=6 and 6 is a perfect number (mathematically...), which probably doesn't make sense to you, but 1/7=0.142857142857142857...., which repeats after 6 decimals ('because' 7 is a prime number and 7-1=6...the exact explanation requires the knowledge of cyclic groups...) and notice how you made 7 the center of a 6-sided circle...)
Looking at it from a distance, I see that you assign the ( allegedly perfect) number 7 to the Default Blender Cube, while it has 6 sides....Blender must be perfect, I guess 🤗
But, considering a week as a 7 day cycle with the seventh day as a resting day, your visual picture looks like a bit of a bumpy ride to me me1958424 .
Unfortunately, we cannot ask Ramanujan (who 'came up' with incredible formulae which he didn't/couldn't prove and claimed they where 'given' to him by God) about this, but he did leave us with (for instance) this:
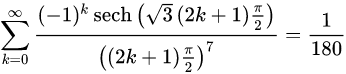Notice the use of the number 7 here!I am correct in saying that the honeycomb shape I used to represent this idea is one of geometric strength?
then the next step is that the perfect number 6 is made complete in that it includes/produces the seventh of them when completing the cycle/circle...
including the idea of infinity in the cyclic number when the 1/7 is carried out...
is there a corresponding upscale infinite number?
I love the math by the way, just not as well versed in it as you are...
me1958424 I don't know a lot about geometrical representations of numbers (if that interests you, you could watch Mathologer's videos. For instance: https://www.youtube.com/watch?v=9JN5f7_3YmQ but they are all fun...), but I don't see a circle in your honeycomb filled with numbers, but more a spiral; the next size would be something like this:
wouldn't it?
Btw. 7 and 19 are called 'centered hexagonal numbers' .
is there a corresponding upscale infinite number?
If I understand you correctly, of course there are many.
For instance: 29 is a prime, so 1/29 repeats after a number of digits, that is a divisor of 28 (which is the second mathematical perfect number, after 6, but that is irrelevant for this construction) and happens to be 28 itself.
Namely 1/29 = 0.34482758620689 65517241379310...... the sequence then starts repeating at the dots. Notice how I put a space halfway. Can you see why? (Look at 1/7 first, if you don't see it immediately...)
spikeyxxx you represented the 19 as center what does the 7 as centered hexagonal look like?
the fractions represent an infinite repeat going down to infinitely smaller...
is there a number that represents the same thing getting infinitely larger?
I like the Mathologer though he gets past me easier than I might care for :D
what does the 7 as centered hexagonal look like?
That would be your drawing.
the fractions represent an infinite repeat going down to infinitely smaller...
I'm sorry, I don't understand what you mean by that, so I can't answer your next question.... Every fraction either repeats infinitely, or has a finite number of digits, like 1/4 = 0.25...(you can fill in any amount of zeros after the 5). The first happens, when the greatest common divisor of 10 (because we are using the decimal system!) and the number you are dividing by, is 1 (they have no common factor).
spikeyxxx and me1958424 I'm fascinated by your mathematical conversation 😀! That's definitively something which I'll revisit for a more in-depth look! And it began all with a bird 😉😁🐦. Kent @theluthier couldn't foresore what his incidental remark would trigger many years later 😉.
spikeyxxx and me1958424 I'm looking forward to more of your mathematical knowledge and findings 😀.
spikeyxxx the fractions represent an infinite repeating pattern going down to infinitely smaller...
and you point out, that is governed by the odd or even condition of the denominator...
fascinating that the 1/7 fraction repeats on a 6 digit pattern... is the denominator -1 a constant pattern?
(you put the space in the 1/29 pattern to indicate the number of digits before repeat being 28?)
is there an infinite repeating pattern that goes larger?
(something tickles about the golden ratio and the spiral it produces... and moving it into 3D space rather than the 2D pattern we use it to represent...)
(it's an idea that has not yet reached completeness in my mind...)
duerer I'm of the mindset that the mathematical patterns we see are intertwined with the theological things you spoke of...
me1958424 did you mean, that you can get a fraction a/b as small as you want, while it still would be repeating a sequence of digits?
In that case, you can, it is even extremely simple; just write any natural number and repeat its digits infinitely...
But, that wouldn't have any of the nice properties, that fractions have.
For instance: 1/7 = 0.142857..., like we already established, but multiplying this by a natural number, cycles through those digits!
2/7 = 0.285714... 5/7 = 0.714285... and so on.
You would not have something like this, when you'd divide one of those infinitely large numbers.
The thing is, I think, that those large, repeating numbers are constructed, while the fractions repeat naturally....I hope that makes some sense to you :)
you point out, that is governed by the odd or even condition of the denominator...
not really the odd/even condition, but whether there is a common factor between 10 and the divisor (when the fraction itself is in its 'simplest' form...)
fascinating that the 1/7 fraction repeats on a 6 digit pattern... is the denominator -1 a constant pattern?
It is, when the divisor is a prime number!
It could have been a 1 digit pattern, a 2 digit pattern, a 3 digit pattern, or a 6 digit pattern, because those are the divisors of 6.
Let me try to clarify this, without going into abstract algebra and group theory too much.
The following applies to all primes that are not 2 or 5 (because those are divisors of 10...), but we will concentrate on 7, for simplicity.
Now, 1/ 7 is something and 2/7 is something else and so on...but then something amazing happens: 7/7 = 1.00000000...
8/7 = 1 + 1/7
So, considering only what happens behind the decimal point, in the case of dividing by 7, the only interesting cases are:
1/7, 2/7, 3/7, 4/,7, 5/7, 6/7. And if you care to count them, that are 7-1 = 6 cases!
Let me now remind you of doing long division (I hope that is what you call them):
It might look something like:
7/1.00000...\ 0.142
7
30
28
20
etcetera...
If you know anything about modulo, you would recognize that 20 is congruent to -1 modulo 7 (3*7 - 1) and that means that 20² is congruent to 1 modulo 7
While writing this, I realize, that all this is going to be more confusing than enlightening, but let's try a bit more...
Suppose, that 100000/7 would yield a rest of 1 (there would exist a natural number n, so that 100000 = n*7 + 1), then in the above long division, there would be a 1 at the fifth decimal, meaning the digits would start to repeat themselves...
but, they obviously repeat themselves after 6 digits (
'So, considering only what happens behind the decimal point, in the case of dividing by 7, the only interesting cases are:
1/7, 2/7, 3/7, 4/,7, 5/7, 6/7. And if you care to count them, that are 7-1 = 6 cases!'
), so if they repeat after 5 and 6 digits, they must repeat after 1 digit. Try all cases and you will hopefully get a feel for why the
number of digits, when 1/p, with p being a prime, not equal to 2 or 5, repeats after a number of digits, that is a divisor of p-1.
Don't worry if you don't, I had a lot more mathematical knowledge when my math professor first showed this to me and I thought he was doing magic ;)
"The thing is, I think, that those large, repeating numbers are 'constructed', while the fractions repeat 'naturally.'..."
when you say constructed and occur naturally is a large help...
the construct is "man made"?
I follow the basic arc of the modulo part but as you noted I probably do not know enough math to take it in in it's entirety...
understood about it appears to be magic :D
...and here is another great channel, if you want to get an idea of modern number theory/ abstract algebra:
All the math here is explained clearly and accurately (and it will probably make your head spin, but don't worry about that ;) eventually things will start to make sense and you might become a magician yourself)